Testes diagnósticos existem para determinar presença ou ausência de doença quando um indivíduo apresenta sinais ou sintomas. Exemplificando para o caso do novo coronavírus, SARS-CoV2, nome dado à doença Covid-19 vinculada à pandemia que assola o mundo, há, portanto, quatro situações a observar: pessoas infectadas que tiveram um exame positivo (verdadeiro positivo), pessoas não infectadas que tiveram um exame positivo (falso positivo), pessoas infectadas que tiveram um exame negativo (falso negativo) e pessoas não infectadas que tiveram um exame negativo (verdadeiro negativo).

A observação destas situações não é nova, e infelizmente nem sempre é possível ter acesso a informações sobre como funcionam tais testes. Em termos lógicos, ao se efetuar um teste para qualquer doença, somente existem duas resultados: ou se está doente, ou saudável. E cada teste tem duas possibilidades: ou é positivo, ou negativo. De fato, o filósofo grego Epíteto (c. 50 – c. 135), havia deixado em sua obra “Discursos”, escrito por volta do ano 108 de nossa era que “as coisas são o que parecem ser; ou não são, mas parecem ser; ou são e não parecem ser; ou não são, nem parecem ser”. Esta descrição filosófica sobre coisas corresponde exatamente às situações de estar doente ou saudável tendo feito um teste com duas possibilidades de resultado: positivo ou negativo.

O exemplo a seguir é meramente ilustrativo e intuitivo, apenas para mostrar como de fato testes diagnósticos são considerados. Tais testes são importantes, ainda que não livres de erros. E também pretende-se deixar claro que não serão considerados marcas ou mesmo tipos de testes, e sim como se comporta a matemática por trás do diagnóstico.

Tais testes correspondem a aplicação da teoria da probabilidade, um belo e importante ramo da matemática, que costumeiramente trata de questões absolutamente amplas e fundamentais. Particularmente, para o caso de análise diagnóstica de uma pessoa após efetuar um teste, a regra a ser descrita adiante trata de como analisar evidências, e mudar de opinião à medida que novas informações surgem, visando tomar decisões racionais. Esta lei matemática foi escrita por um reverendo presbiteriano, deixada numa carta póstuma, que provocou uma revolução no modo de pensar. Foi publicada numa das primeiras revistas científicas do mundo, num artigo de título: ‘Um Ensaio Para Solucionar um Problema na Doutrina das Chances’ (“An Essay Towards Solving a Problem in the Doctrine of Chances”) em 1763, assinada pelo pastor inglês Thomas Bayes (1701 - 1761).

Este enigmático reverendo, de quem tem-se pouquíssima informação, tratou de compreender melhor, em termos matemáticos, uma inflamada controvérsia religiosa de sua época: seria possível tornar racional conclusões sobre Deus baseadas em evidências a respeito do mundo que nos cerca?

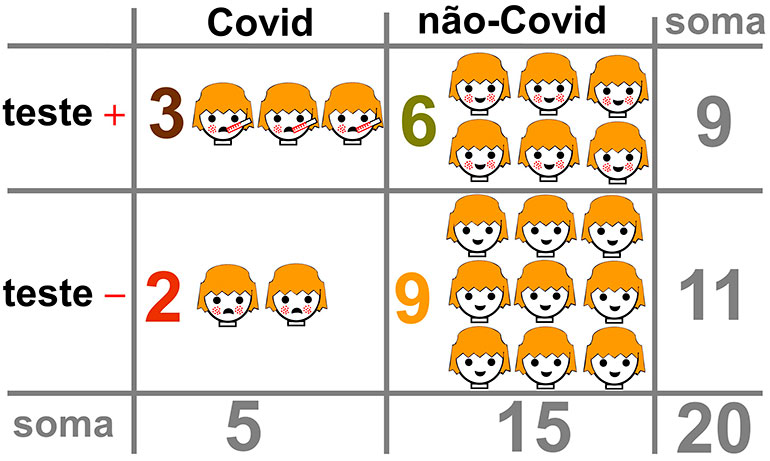
Deixando esta questão para um outro momento, pretende-se tratar dum exemplo meramente ilustrativo de situações sobre pessoas com e sem covid, tendo efetuado testes que resultaram positivo ou negativo. É fácil perceber que existem apenas quatro resultados entre ter ou não covid combinados com os resultados dos testes: i) com covid e com teste positivo (verdadeiro positivo); ii) sem covid e com teste positivo (falso positivo); iii) com covid e com teste negativo (falso negativo); iv) sem covid e com teste negativo (verdadeiro negativo). Neste caso fictício vamos considerar três pessoas com covid e teste positivo, seis sem covid e com teste positivo, duas com covid e com teste negativo, e nove sem covid e com teste negativo, resultando em vinte pessoas.

Dos dados fictícios é primeiramente importante notar o quanto existe de gente doente (cinco com covid) e saudável (quinze sem covid) e quantos testes são positivos (nove) e negativos (onze), sendo que foram consideradas vinte pessoas. Ainda que fictício, houve um esforço de se propor uma prevalência de menos infectados por covid e de casos negativos em maior número que os positivos, algo que se espera no geral.

Os dados permitem responder a algumas questões interessantes, como por exemplo qual é a probabilidade do teste dar positivo caso alguém esteja com covid. No entanto, uma pergunta mais pertinente seria se o teste der positivo, qual a probabilidade de alguém estar realmente doente?

É importante notar que tais questões são diferentes. Bayes propôs por meio de sua teoria um modo de efetuar questões condicionais, com isto se aproximando do modo de pensar da humanidade, que em geral efetua julgamentos ditos bayesianos. Em outras palavras, a questão bayesiana é: qual a probabilidade de alguém estar doente dado que o teste deu positivo?

Uma maneira de responder a este problema de faz-de-conta é: caso o evento covid tivesse ocorrido, qual a probabilidade dele ter provido da evidência teste positivo?

A resposta envolve três pessoas que apresentaram teste positivo para covid entre as nove que testaram positivo, resultando em 3/9, 1/3 ou ainda aproximadamente 33,3%.

Em essência, este é o cerne do Teorema de Bayes, denominado de problema da probabilidade inversa. Em termos gerais, este teorema estabelece uma relação entre causa e efeito – a probabilidade de uma causa (dado um evento) é proporcional a probabilidade de um evento (dada esta causa) – bem como das probabilidades da causa e evento, ambas em separado. Em termos práticos, basta tomar o teorema e substituir a causa (covid) e evento (teste positivo) para compreender um pouco mais sobre o que o reverendo tinha a dizer.

Portanto, em termos gerais, a probabilidade de ter covid dado que o resultado do teste foi positivo (a chamada probabilidade posterior), está relacionada ao produto da probabilidade do teste ser positivo dado que proveio de alguém com covid (isto pode vir dos dados ou ainda do conhecimento médico) vezes a probabilidade de ter a covid (um dado que pode estar vinculado à observação da doença num período ou ainda proveniente puramente dos dados) dividida pela probabilidade de se obter um teste positivo (que de fato corresponde ao exame médico).

Enfim, testar ou não testar não se trata de uma questão shakespeariana. Testar é preciso e necessário, seguindo a receita camoniana. Matematicamente falando, a testagem consiste num resultado médico. Cabe ao especialista em saúde, com base em conhecimento matemático definido por Bayes, estabelecer o melhor diagnóstico possível.

Num período onde as vacinas para Covid-19 ainda não são disponibilizadas para todos, a testagem da população é mais do que urgente – é fundamental, mantendo-se, é claro,  o distanciamento social e o uso de máscaras.